dummy

数字逻辑与数字系统

基础知识

逻辑门

单输入逻辑门

image-20210309155515553

两输入逻辑门

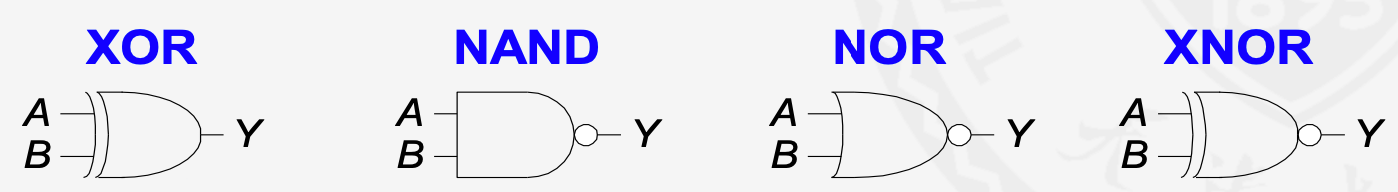
多输入逻辑门

就是多个入口

CMOS晶体管

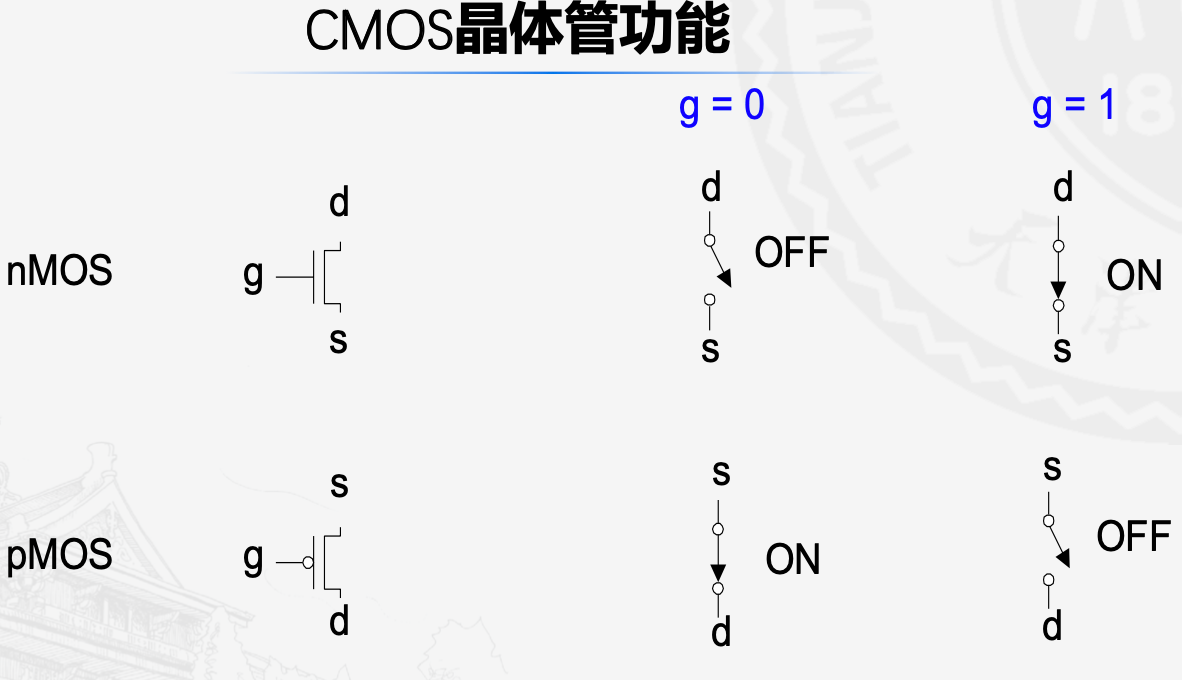
image-20210309155658379

nMos能够很好的导通低电平0，因此源极接地

pMos能很好地导通高电平1，因此源极接电源

CMOS非门和CMOS与非门

和非门与非门没啥区别。

组合逻辑设计

引言

数字逻辑电路

是一个可以处理离散值变量的网络

有输入、输出、功能规范和时序规范

结点和模块

结点是一段导线，通过电压传递离散值变量

输入节点
输出结点
内部结点

模块本身是一个带有输入、输出、功能规范和时序规范的电路

数字逻辑电路的分类

组合逻辑电路
任一时刻的输出仅由该时刻的输入信号决定
无记忆
时序逻辑电路
任一时刻的输出由该时刻的输入和电路该时刻的状态共同决定
有记忆

组合逻辑电路

每个电路模块都是一个组合逻辑电路
每个电路结点要么是输入，要么只连接一个电路的一个输出端
电路中不包含回路

布尔代数

值：0或1
计算：与(·)或(+)非($\overline{A}$)

最大项$M_i$和最小项$m_i$

蕴含项

项的乘积

最小项

包含全部输入变量的乘积项

$m_i$为使最小项为1所对应的等效十进制数

例如$m_3$中，为ABC组成的变量的二进制数为3，即A,B,C = 0, 1, 1

最大项

包含全部输入变量的求和项

$M_i$为使最大项为0所对应的等效十进制数

例如$M_3$为A,B,C = 1,仍然是A,B,C = 0, 1, 1，只是表达式为$ A + + $

与或式和或与式

就是先与后或或者先或后与

例如$A+BC$为与或式，$(A+B)C$为或与式。

标准与或式

对于由最小项之和构成的逻辑表达式可以有以下简化表达形式

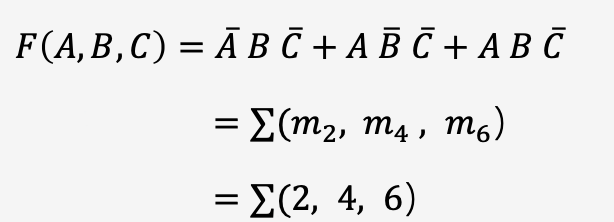
image-20210622170604629

布尔表达式与真值表的转换

image-20210312104532650

从逻辑到门

需要掌握：从布尔表达式画门；优先级电路

挺简单的，看看PPT就成，注意要遵循画图逻辑，比如左上进右下出，T型图没有点，交叉电路连接带点不连接不带。

多级组合逻辑

减少硬件

转化为与或式
采用多级逻辑

可以减少门电路数量
减少扇入数

推气泡

从输出端往输入端推
CMOS中常常使用与非门和或非门
气泡可以通过德摩根定律在与门或门的前后转换
一根导线上前后都有气泡可以抵消

X和Z

可以用于非法值或者无关项。

浮点值，表示可能为0或1输出不确定。不意味着电路一定出错。

三态缓冲器

在buf上多出一根线，表示使能端

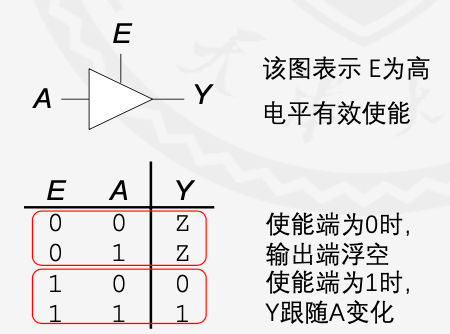
image-20210312112254689

当一个结点有多个输出时，只有一个输出为有效状态，其他为浮空时，该结点取正常输出的值。

卡诺图

包含小方块的几何图形

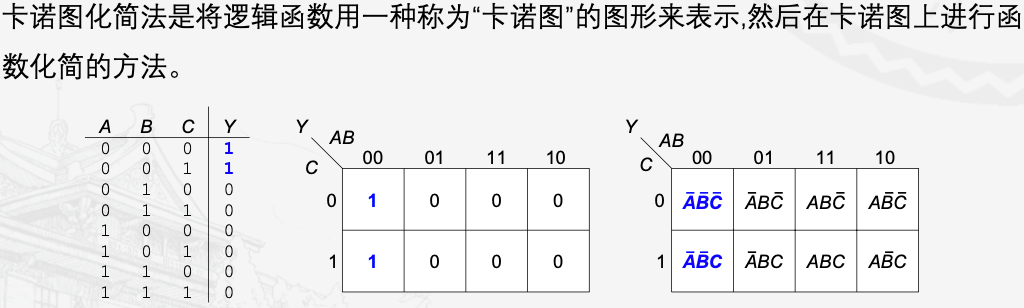
image-20210312111935968

合并最小项

标1的方格相邻可以合为一项
四个相邻可以消去两个（田字/一条线）
有八个相邻可以消去3个（2*4)

即，在有n个变量的卡诺图里，若有矩阵形2^i个相邻的值为1的方格，可以消去i个变量，留下n-i个变量。

卡诺图化简

注意在有无关项在卡诺图中时，如果圈住有利于化简，就圈进去，否则不圈。

组合逻辑模块

编码器

用n位二进制代码表示2^{n位输入，即输入2}n位，输出n位

例如对4-2编码器进行分析，首先编码器的作用是把输入最高位的1的位数用二进制表示出来，例如输入0101，即最高位为第2位(从0开始)，所以输出10

然后我们得到真值表，并且画出卡诺图并且化简

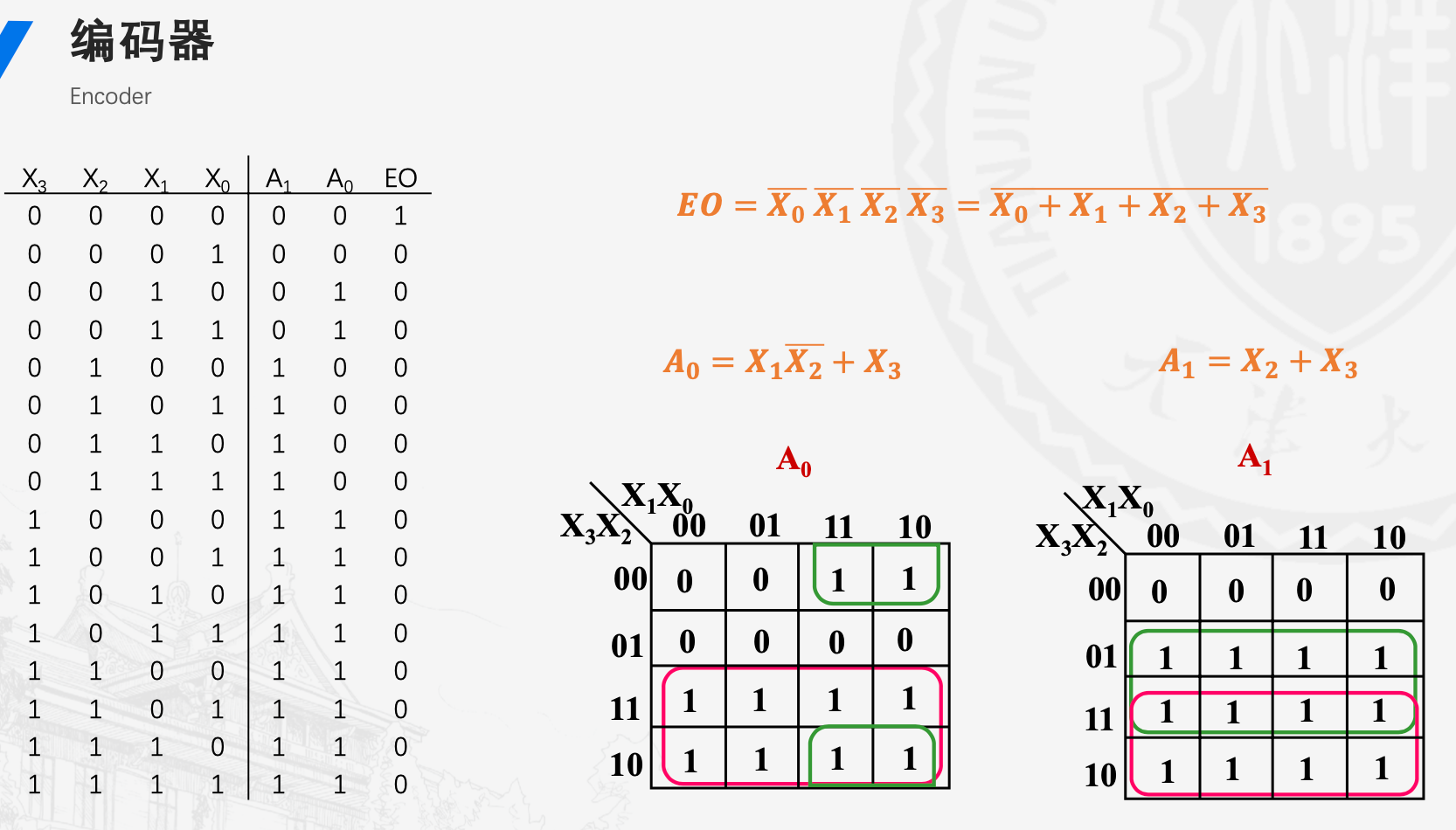
image-20210622172738725

再根据化简后的表达式，画出电路图

image-20210622172813019

译码器

有n个输入，2^n个输出

译码器的输出为独热编码，即输出1<<n

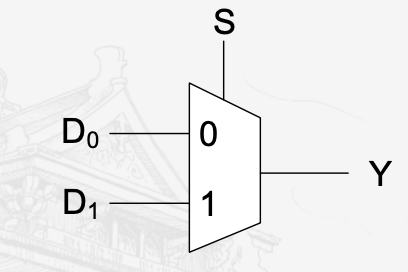
多路选择器

就是书中的复用器，通过使能端判断输出哪一个信号，最基础的是二选一的多路选择器

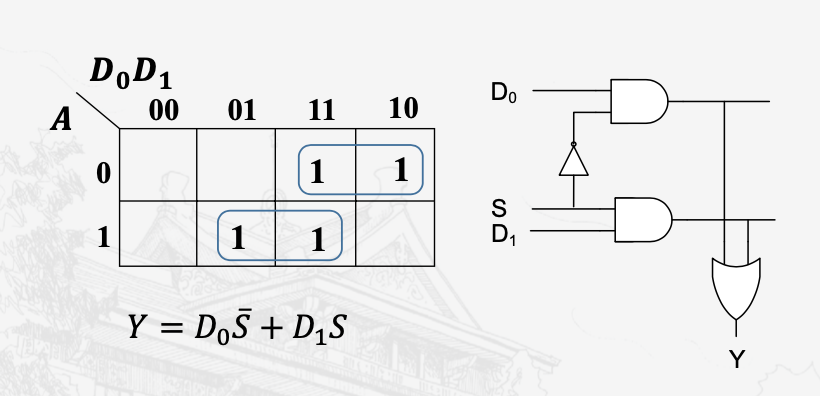
组合逻辑中的时序问题

实际电路中，输出和输入之间具有一定的时延。

所以我们讨论两个延迟

分别为传播延迟$t_{pd}$和最小延迟$t_{cd}$

传播延迟就是从输入开始改变到输出结束改变的时间

最小延迟就是从输入开始改变到输出开始改变的时间

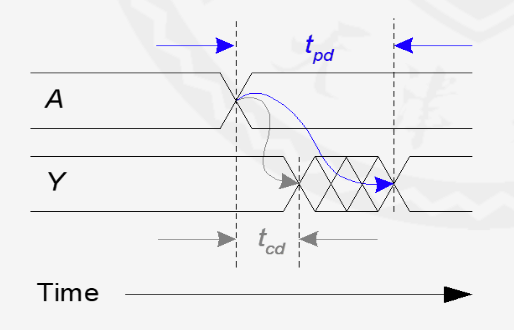
image-20210319103159897

于是我们引出两个路径：

关键路径和最短路径

关键路径指分别指信号传输最慢的路径和最快的路径

毛刺

毛刺是一个输入改变引起输出的多次变化，其原因是是传播延迟和最小延迟导致的

当信号的变化在卡诺图中穿越2个主蕴含项的边缘时会出现“毛刺”

通过增加主蕴含项来盖住边缘可以避免毛刺

SystemVerilog

基本结构

module mux2(input logic D0, D1, sel, output logic y)
  logic a,b;
  assign a = D0 & (~sel);
  assign b = D1 & sel;
  assign y = a | b;
endmodule

一个基本的逻辑电路由module ... endmodule定义，同时须有input和output的定义。

语法要素

逻辑值

0 1 x z，意义如之前所述，x为不定值或者未知值，z为高阻态即浮空值

常量

常量的格式为<+/-><位宽>'<进制><数值>，例如-3'b101即为负的位宽为3的二进制的101

进制默认为10进制，位宽默认为给定数字的宽度。

数据类型

有变量类型和线网类型。

变量类型主要包括logic,bit,byte,shortint,int等，其中只有logic有四种状态，其他只有01。

向量定义（类似数组）为logic [15:0] addrbus, databus，定义了一个16位的信号与一般语法有点不太一样，大的在前小的在后。

域选（切片）语法为assign out[7:0] = in[7:0]，即0到7位的赋值。

其他类型的简单定义。

image-20210326110419210

线网类型包括wire,tri等，tri可以定义多元驱动信号

module tristate (input logic a, input logic en, output tri y)
  assign y = en? a : 1’bz;
endmodule

运算

基本运算和编程语言大同小异，主要介绍下缩减运算、拼接和无符号数和有符号数之间的运算。

缩减运算指&、|、^、~，与或异或和同或，对一个信号的每位进行该运算。

例如 ^b101，即1 ^ 0 ^ 1 = 0。

拼接指类似于 { A, B }的语法，会将A和B头尾相接，同时支持{ n{A} }这样的重复操作，A后面也可以进行域选，例如 { A[3:0], 3{A[0]} }

行为建模

基于持续赋值语句的建模

持续赋值就是使用assign <#n>... = ...的形式组成的逻辑电路，其中每个变量在输入变化时也会变化。可以加上#n以表示延迟

基于过程块的建模

过程块就类似高级语言了，有if else case等。

always过程块分为三种类型:always_comb(描述组合逻辑)，always_ff和always_latch(描述时序逻辑)。然而现在只用到always_comb。

结构类似于

module
  always_comb begin
    if ...
    else ...
  end
  
endmodule

在过程赋值语句中，不用加上assign，有=（阻塞赋值）和<=（非阻塞赋值）两种，但是也能加上#n的延迟量。

for repeat while forever如下

image-20210326113514102

结构化建模

就是Extract一个View

参数化建模

就是定义常量

测试程序

测试程序由激励信号、DUT和输出响应三个部分组成

测试程序模板如下

module testbench_name(); // testbench为顶层模块，不会被其它模块例化，因此不需要任何端口
  // 信号定义
  // 模块实例化
  // 添加激励信号
  // 显示输出结果(可以不添加任何显示打印语句，只生成波形图即可)
endmodule

添加激励信号

主要有三种方式

initial （线性）
always (循环)
文件

initial

在一个程序中可以有多个initial块，但是块之间是并行执行的，所以不要对一个变量多次更改。

文件

把测试数据放在文件里，使用时读入

  基于SystemVerilog的测试程序
SystemVerilog based testbench
通过文件施加激励
  将激励(测试向量)存放在一个文本文件中，测试程序从文件中读取激励，对DUT进行测试。
module sillyfunction_tb ( );
  logic a, b, c, y;
  logic [2 : 0] stim [7 : 0]; // 声明一个logic类型的数组 int i;
  sillyfunction dut (.a(a), .b(b), .c(c), .y(y));
  initial begin
    $readmemb ("testvector.txt", stim);// 将所有激励读入数组stim
  for (i = 0; i < 8; i = i + 1) begin
    {a, b, c} = stim[i]; #10; // 依次测试各个激励
  end end
  initial begin
    $monitor ($time, “a = %b, b = %b, c = %b, y = %b”, a, b, c, y);
  end
endmodule

输出响应

会用到一些系统相关函数

image-20210402104448532

display和moniter区别在于执行到语句输出或者变量变化时输出

时序逻辑设计

时序逻辑电路的输出由当前时刻的输入和之前时刻的输入共同决定。

锁存器和触发器

这是用于存储1bit状态的模块。

双稳态电路

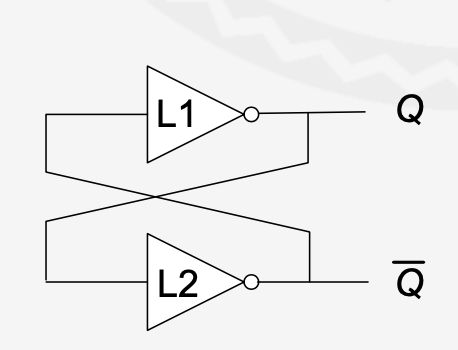
双稳态电路是其他存储模块的基础，其具有对称性，有输出无输入。

Q或者$\overline{Q}$，为0或1时，都是对应一个0一个1的输出。

SR锁存器(latch)

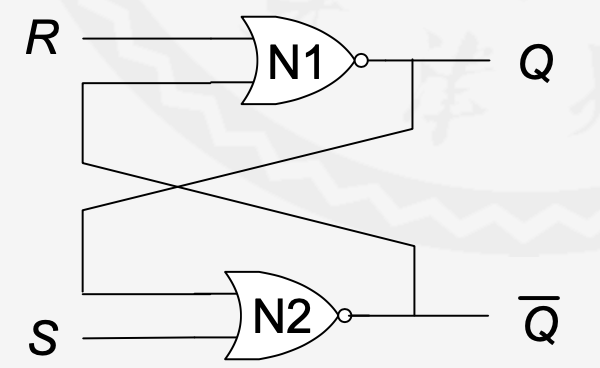
具有两个输入端和两个输出端。

讨论一下输入输出

S	R	Q	Q非	备注
1	0	1	0	置位(set)
0	1	0	1	复位(reset)
0	0	keep	keep	保持态，不变
1	1	0	0	强制Q和Q非为0，无激励信号后恢复

D锁存器

image-20210420155353261

CLK：控制锁存器状态发生改变的时间

D：数据输入控制下一状态的值

当CLK为1时，Q为D，CLK为0时，Q保持状态。

实现过程如下

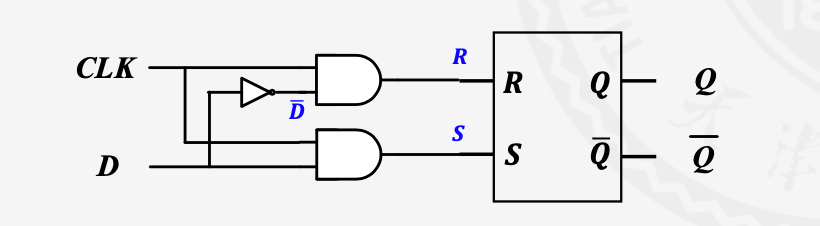
D触发器

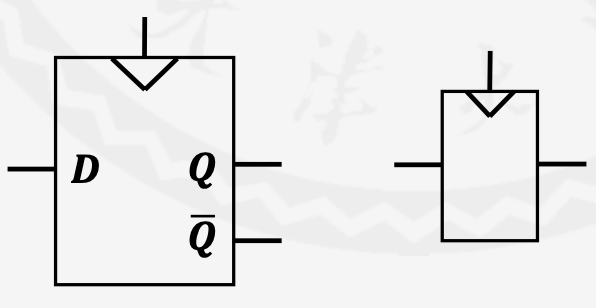
包含两个输入CLK和D

在CLK的上升沿（即0到1时）输出D，其他时间保持

由两个顺序连接的D锁存器构成

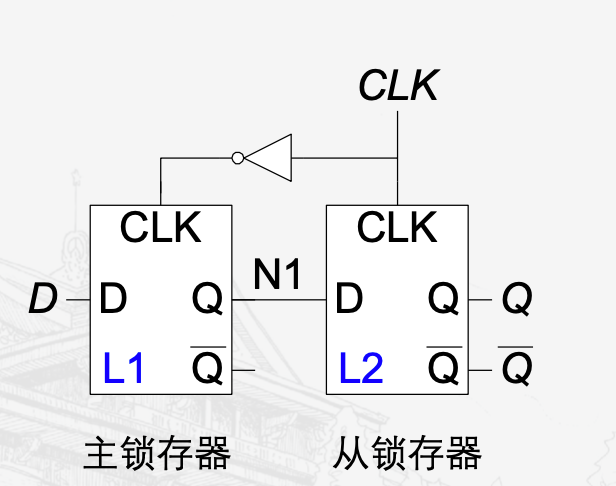
CLK = 0时，L1透明，CLK = 1时L2透明（透明即可变）

故在0变成1时Q赋值为D

寄存器

实现过程还是比较有趣的

带使能端的D触发器

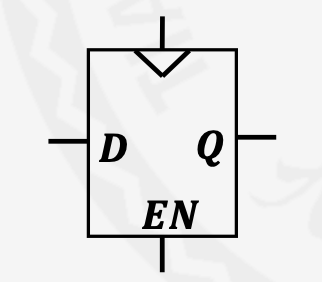
三个输入CLK、D、EN

EN=1时，在时钟上升沿Q被更新，否则保持

带复位功能的D触发器

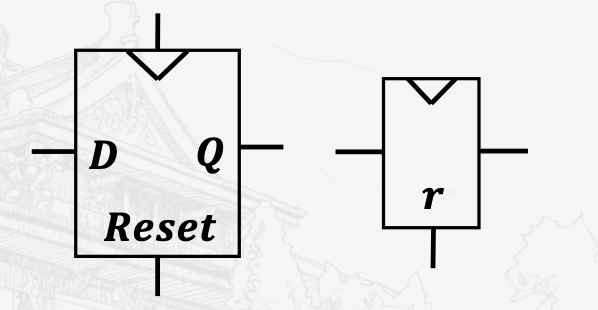
image-20210420161534652

三个输入CLK、D、Reset

Reset = 1时，Q被强制设为0

带置位功能的D触发器

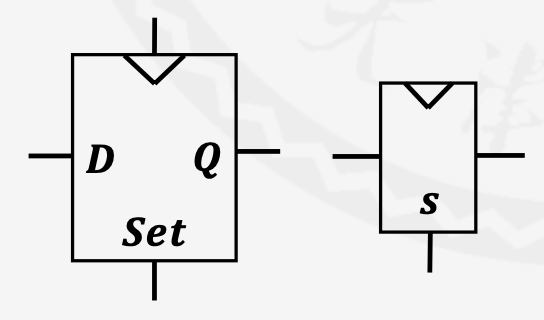
image-20210420161744589

三个输入CLK、D、Set

Set = 1时，Q被强制设为1

同步逻辑设计

时序逻辑电路指所有不是组合逻辑的电路。

同步时序电路

插入寄存器来实现状态保持功能，状态仅在时钟变化发生改变。

有一组有限的离散状态
有一个时钟输入
上升沿表示电路状态转变发生的时间。
具有功能规范和时序规范

组成工作

电路中的模块或者是寄存器或者是组合逻辑电路
模块中至少包含一个寄存器
所有的寄存器都共用同一个时钟信号
电路的每个环路中至少包含一个寄存器

异步时序电路

如果电路里状态的改变都是由同一个时钟信号引起，则为同步时序电路，如果有其他的信号能够引起改变，则叫异步时序电路，比如有always_ff@(posedge sys_clk, posedge reset)，这样的就是异步时序电路。

有限状态机

FSM由状态寄存器和组合逻辑组成。

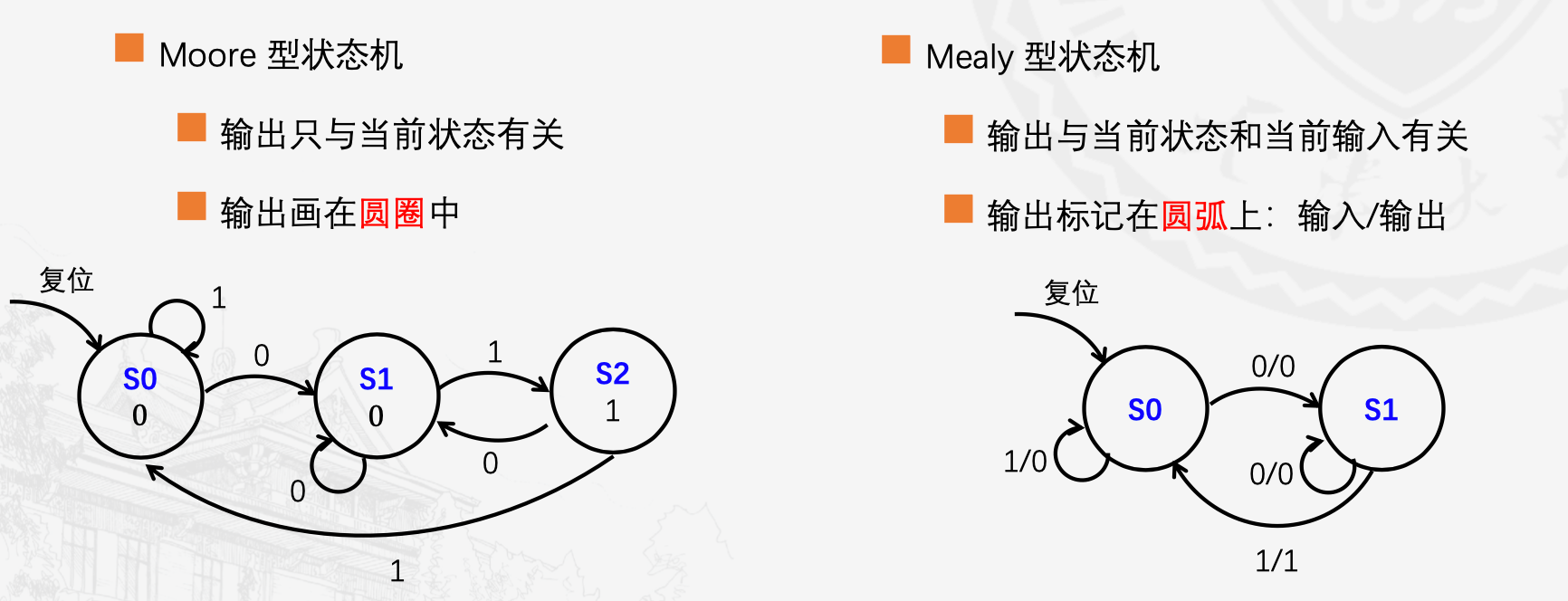
Moore型状态机

输出仅由当前状态决定

Mealy型状态机

输出由当前时刻状态和输入共同决定

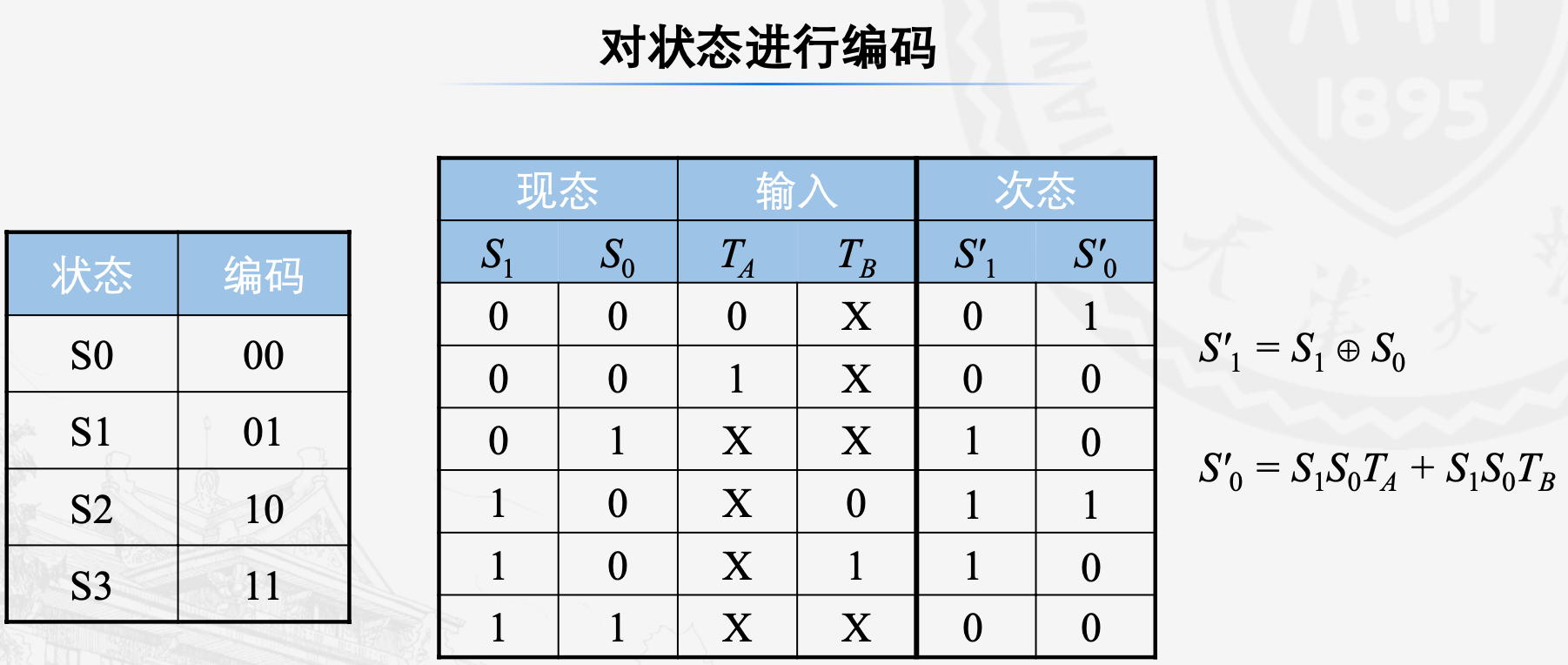
对这一题

image-20210623092231576

有状态转换表如下

image-20210423104436621

再对状态进行编码

image-20210423104817120

于是根据上图，可以写出次态逻辑的电路图/原理图

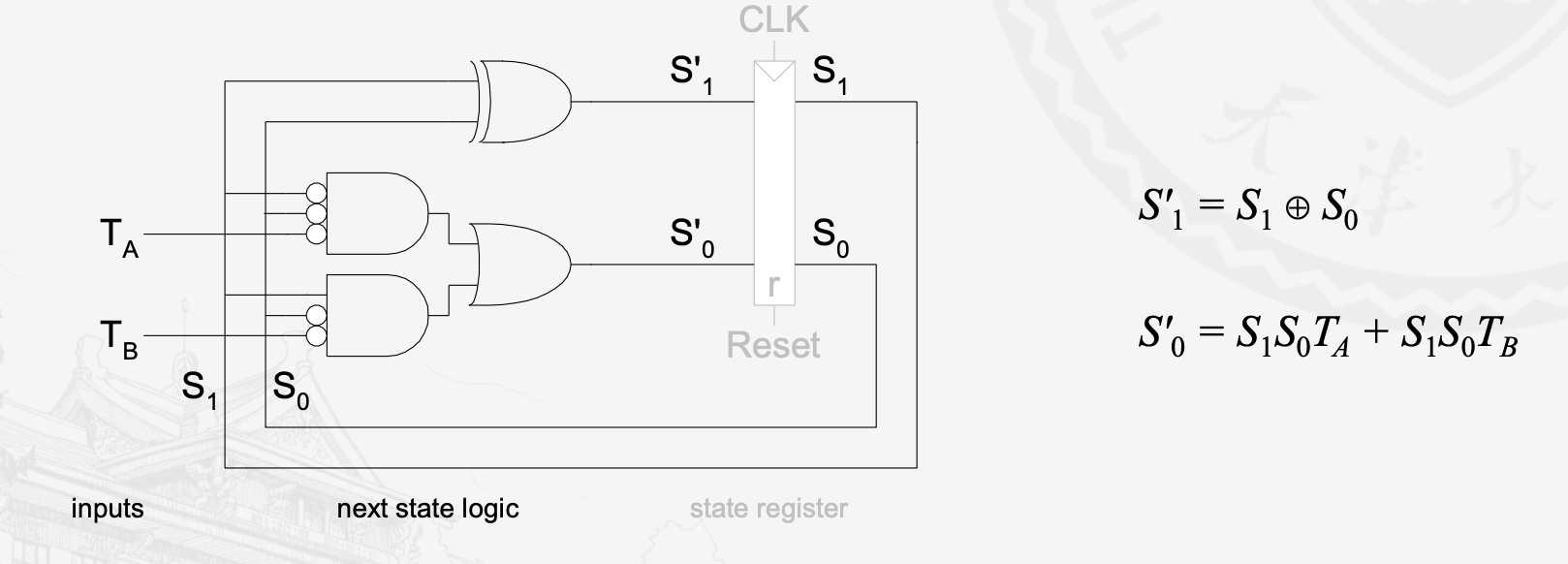
image-20210623095341213

再对输出进行编码

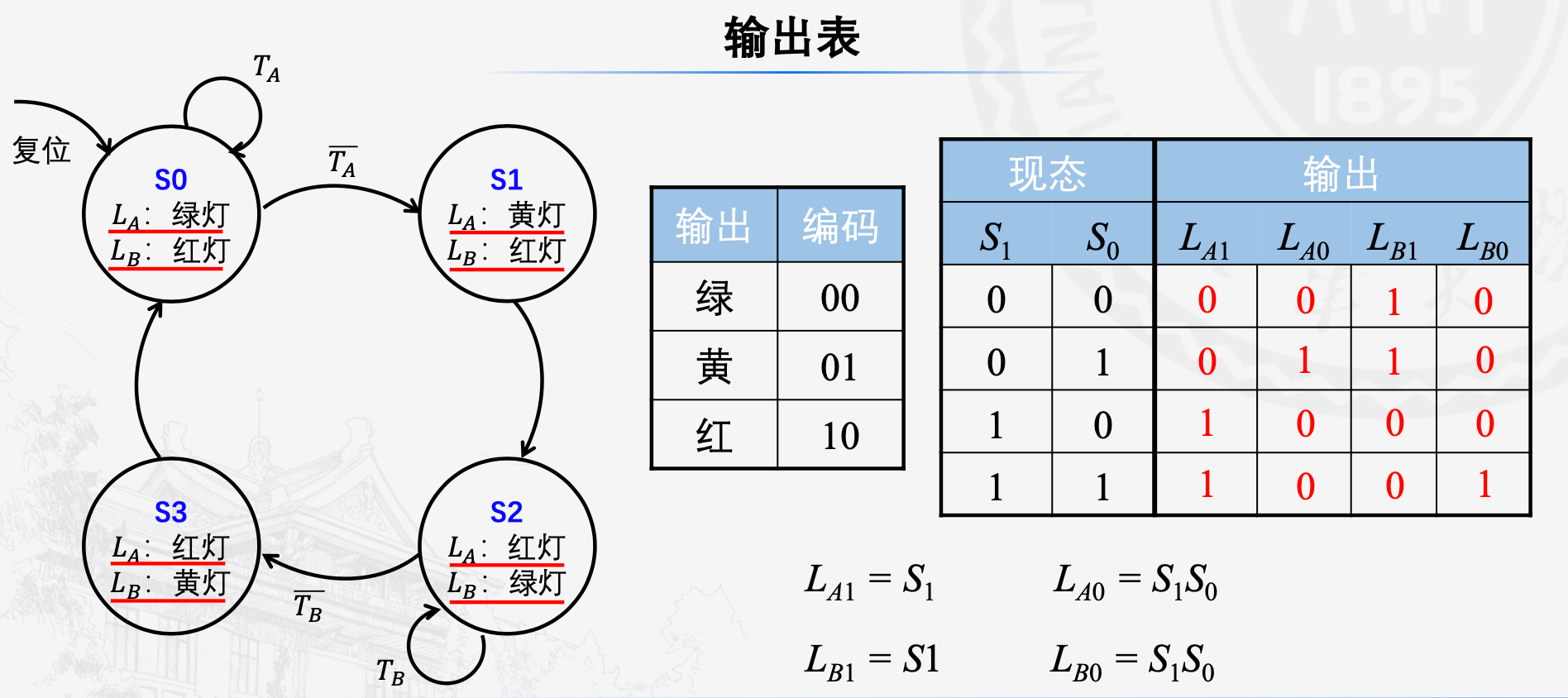
image-20210423105205721

同样，也可以将输出的电路附加到上面次态逻辑的电路上。

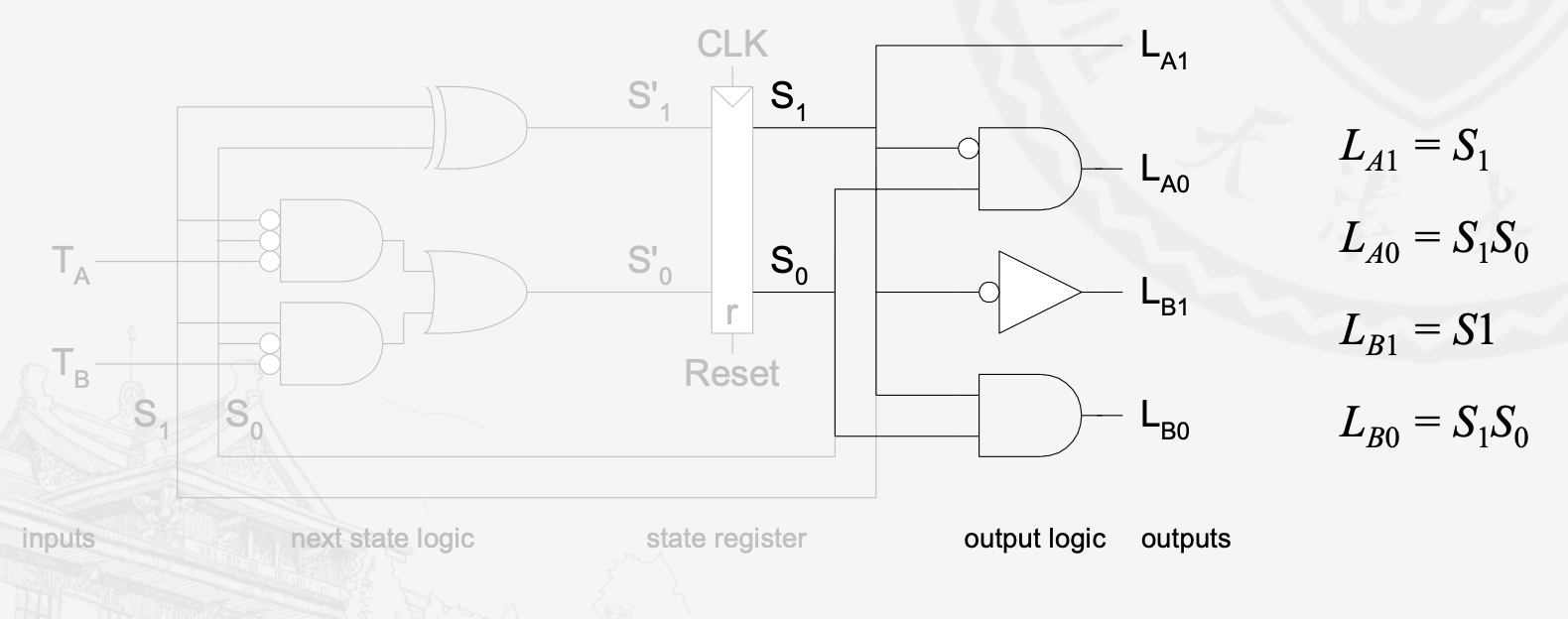
image-20210623095402054

于是我们走了一遍状态机的设计方法

有限状态机设计

Moore型状态机设计

分7个步骤

根据问题进行抽象，确定输入输出以及对应的逻辑含义
画出状态转换图
列出状态转换表
对状态进行编码，并列出次态方程
列出输出表
对输出进行编码，并列出输出方程
绘制原理图

对上面的交通灯问题，我们首先确定了输入：两条道上是否有行人，分别为TA和TB信号，这两个信号位宽为1，只用表示0（没有行人）和1（有行人），输出：两个位宽为2的信号LA和LB，即最少能够表示3钟灯（红黄绿）的信号。

然后画出了Moore型状态转换图，跟着可以列出状态转换表，次态方程也能写出来（有的教材也叫驱动方程），列出输出表时，其实也可以同时对输出进行编码，最后一步绘制原理图中，其实可以分两步走，也就是先画出状态图的电路表，再加上输出的电路图。

Mealy型状态机设计

个人认为Moore型状态机更容易设计，Mealy型的区别在于，他是输出与现态和输入都有关，并且输出在状态转移过程中，设计更难也带来了好处：能够使用更少的状态表示。

以蜗牛题为例

image-20210623102139674

对比Moore型状态机而言，Mealy型能够少写一个状态。

image-20210623102213188

Mealy型状态机的设计过程：

根据问题进行抽象，确定输入输出以及对应的逻辑含义
画出状态转换图
列出状态转换表和输出表(可同时列出)、对状态和输出进行编码，并列出次态方程和输出方程绘制原理图
对状态和输出进行编码，并列出次态方程和输出方程
绘制原理图

对于Mealy型的状态转换和输出，常常是一起列出的

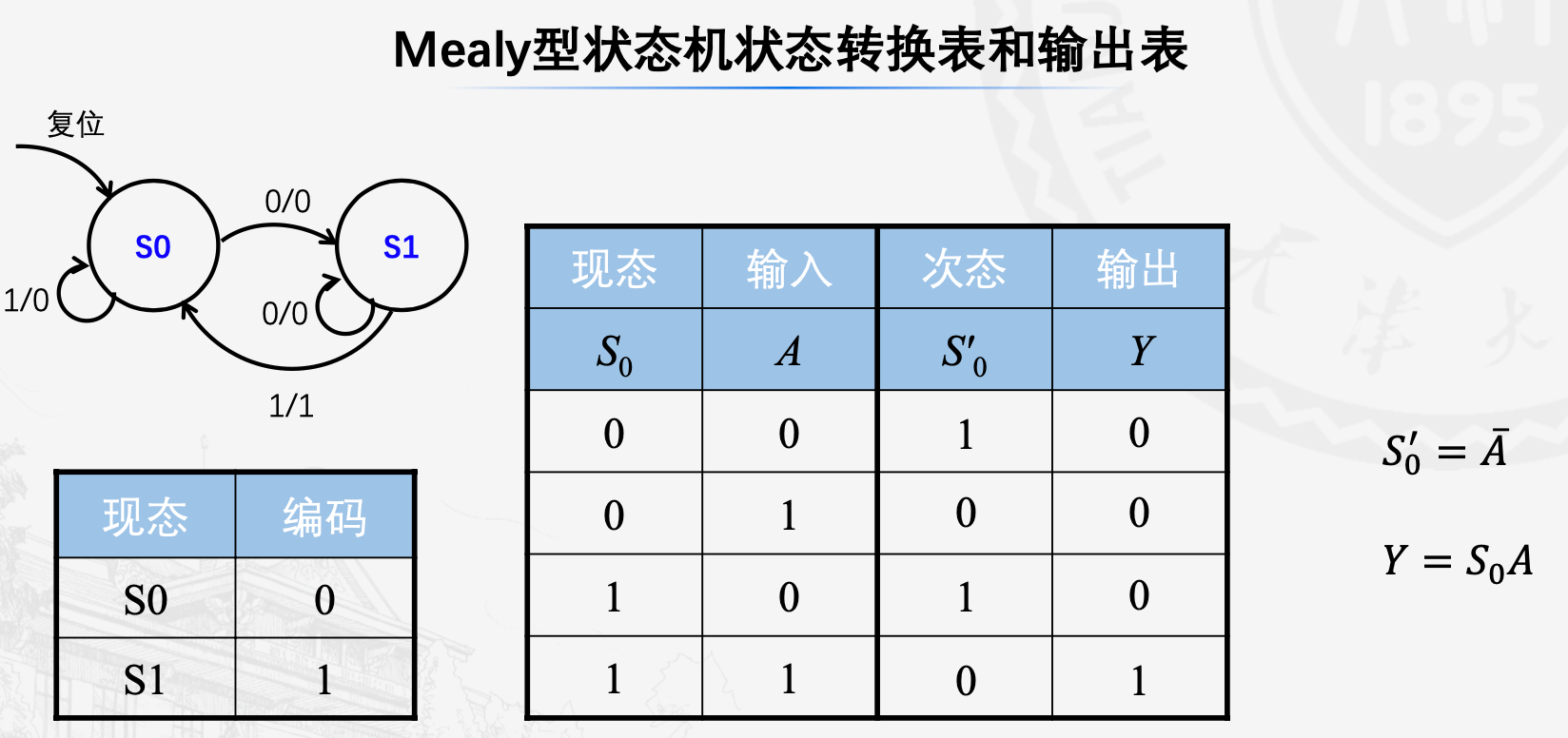
image-20210623110437369

得到原理图

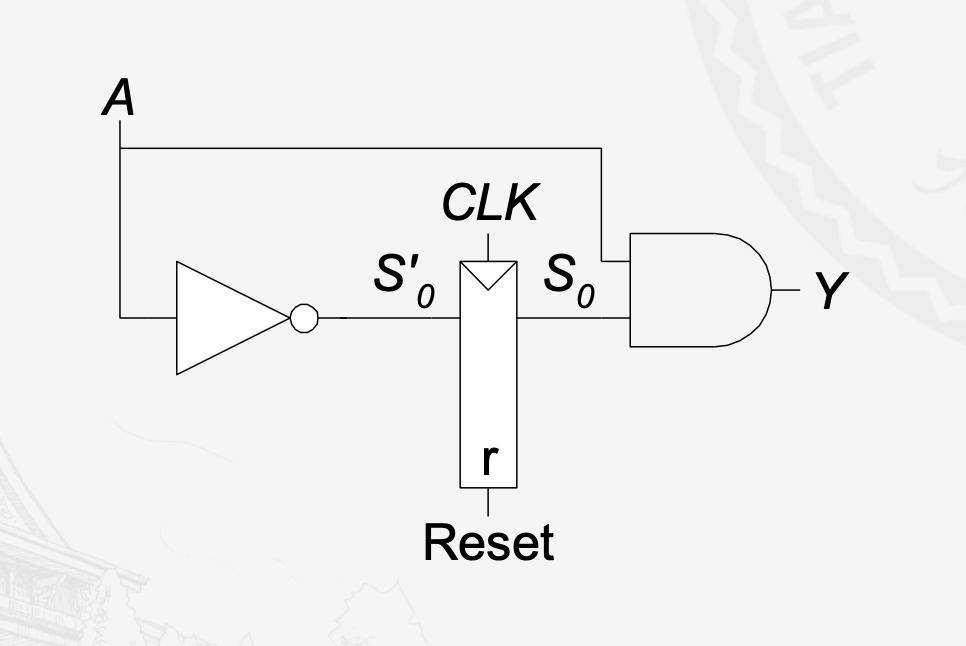
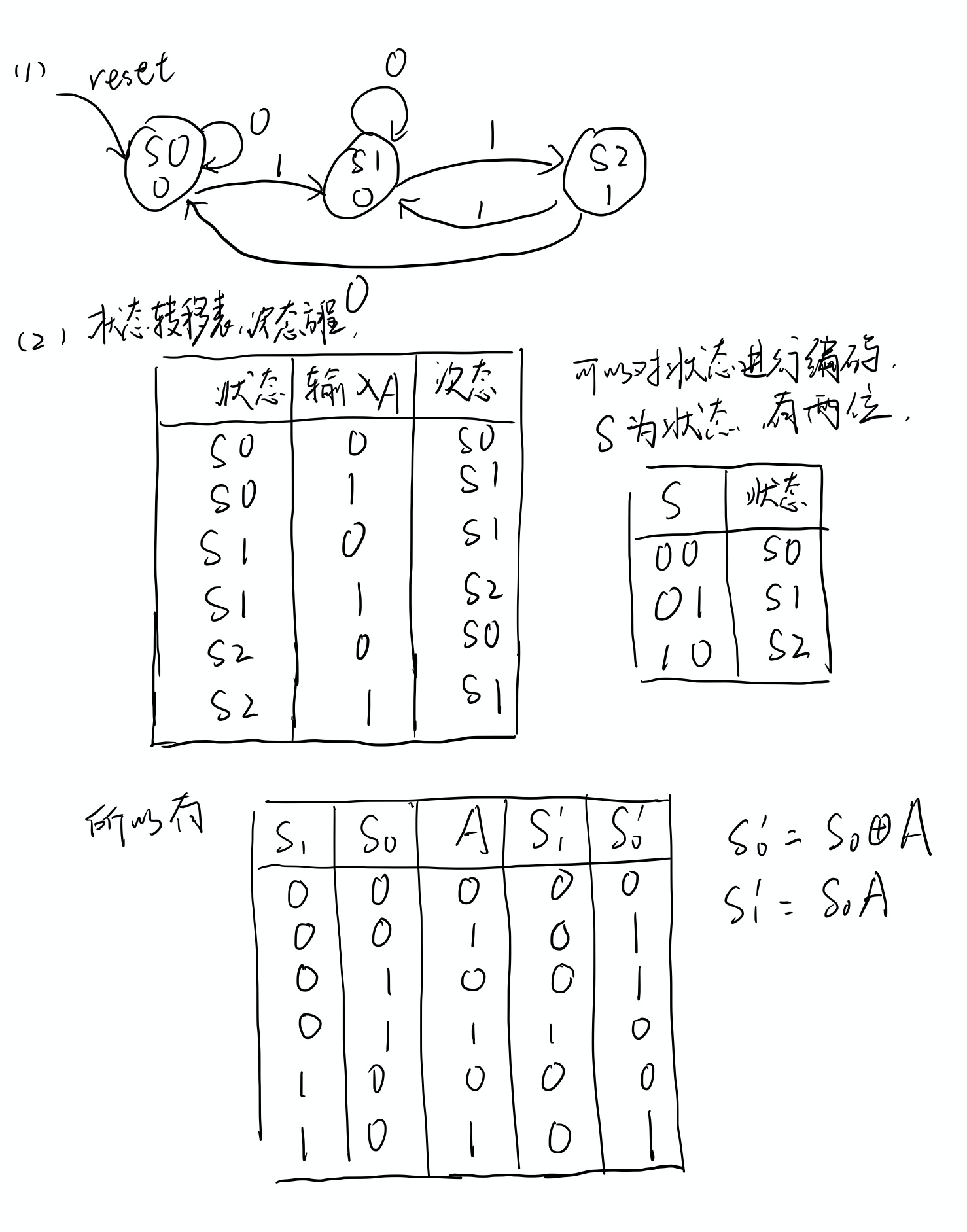
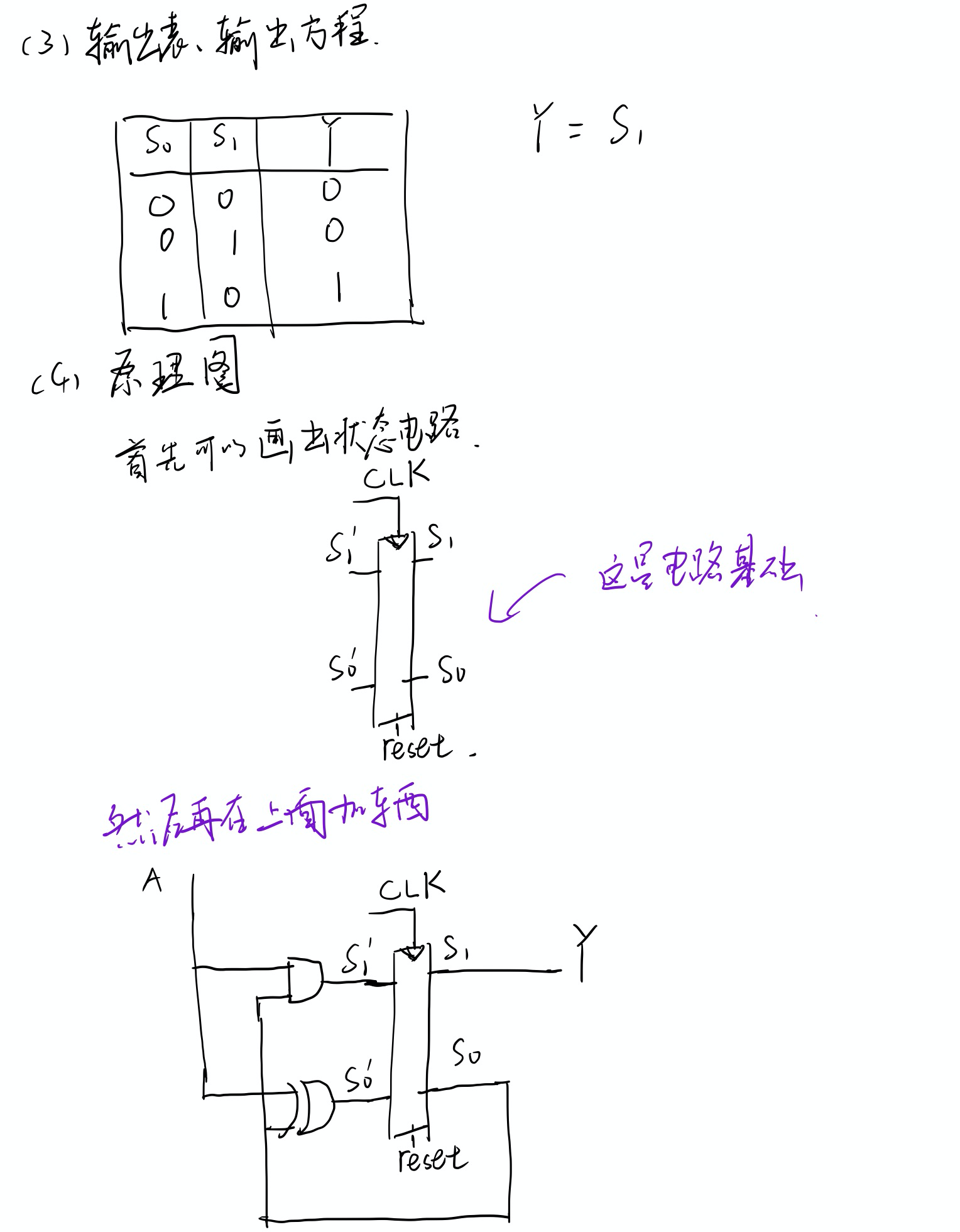
作业：投币机

7EB6369062709BE94773D4258B178F78

Moore型的还是比较简单设计的

image-20210623114047392

image-20210623114201905

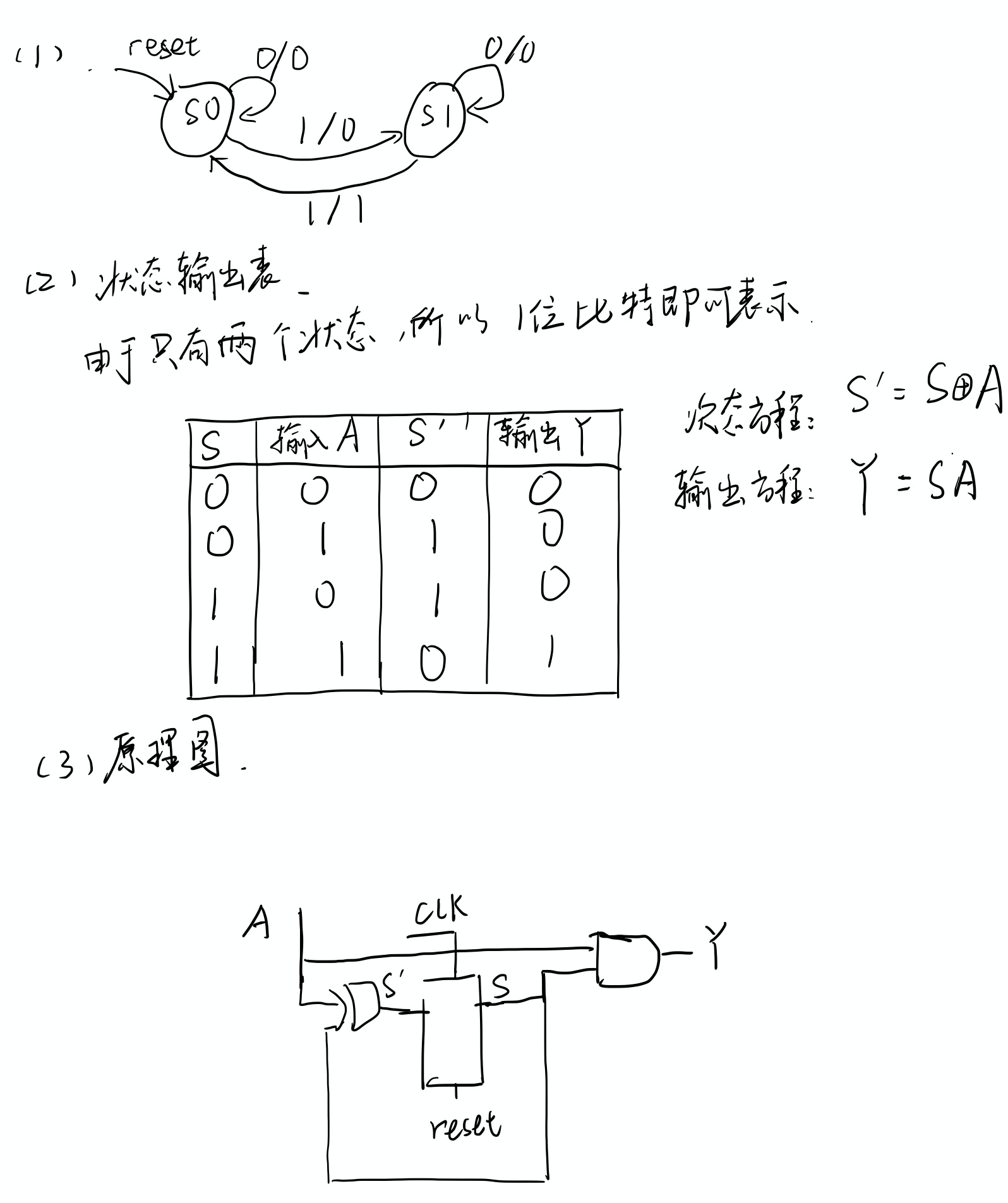
Mealy型能想出来也是很简单的

image-20210623114846910

由电路图导出状态机

由于不考，所以简单了解即可

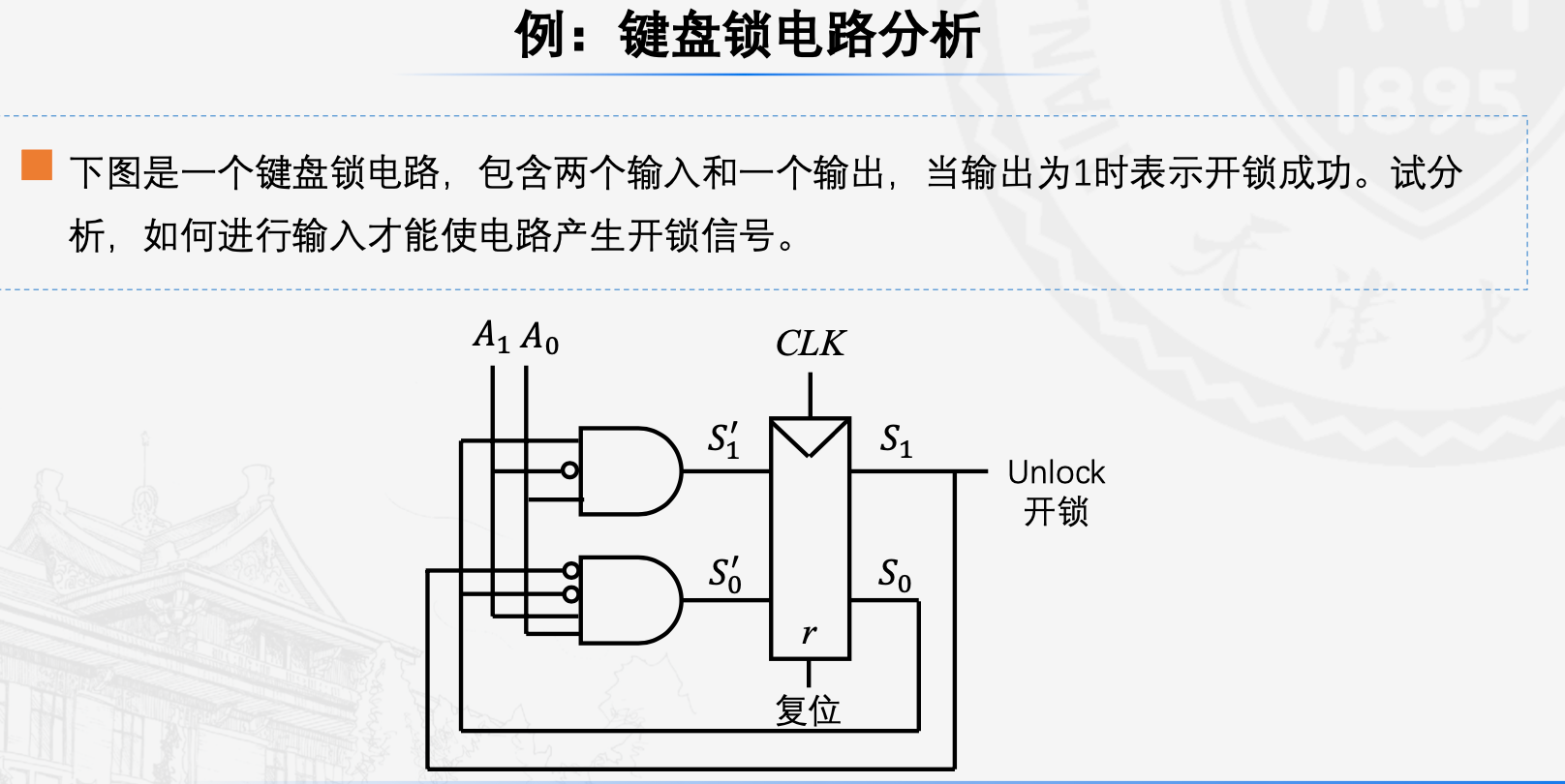
image-20210623115259298

如图，对电路分析可以很简单写出次态方程和输出方程，根据次态方程写出状态表输出表，注意在这一步里，如果可以，去掉多余的状态，进行简化，再画出状态转换图即可。

时序问题

输入时序约束

注意建立时间和保持时间的定义，这里建立时间和保持时间都是对寄存器而言，要保证信号稳定而定义的时间长度，建立时间短了，或者保持时间短了，都可能造成信号采样的不稳定。

输出时序约束

\[ t_{pcq} = t_{cd} + t_{ccq} \]
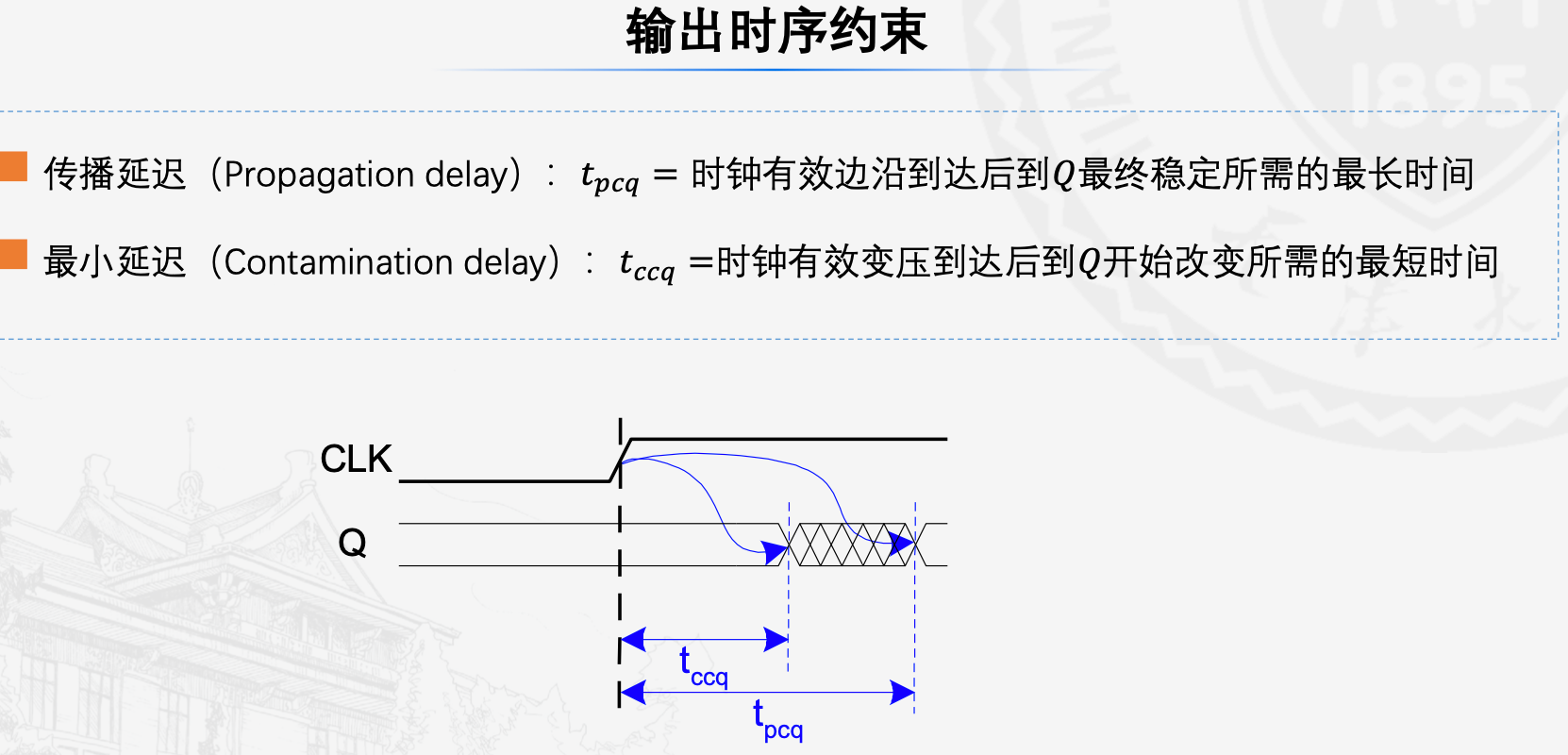
其中$t_{cd}$为组合逻辑的延迟

对于一个时序电路，一般来说，时钟周期Tc是两个上升沿或者两个下降沿之间的间隔，他的倒数fc表示时钟频率。

显然我们要保证，从开始时系统状态开始发生改变，到改变后系统状态稳定的这段时间不得长于一个时钟周期。

建立时间约束和保持时间约束

即有关系
\[ t_{pd} \le T_c -（t_{pcq} +t_{setup}） \]

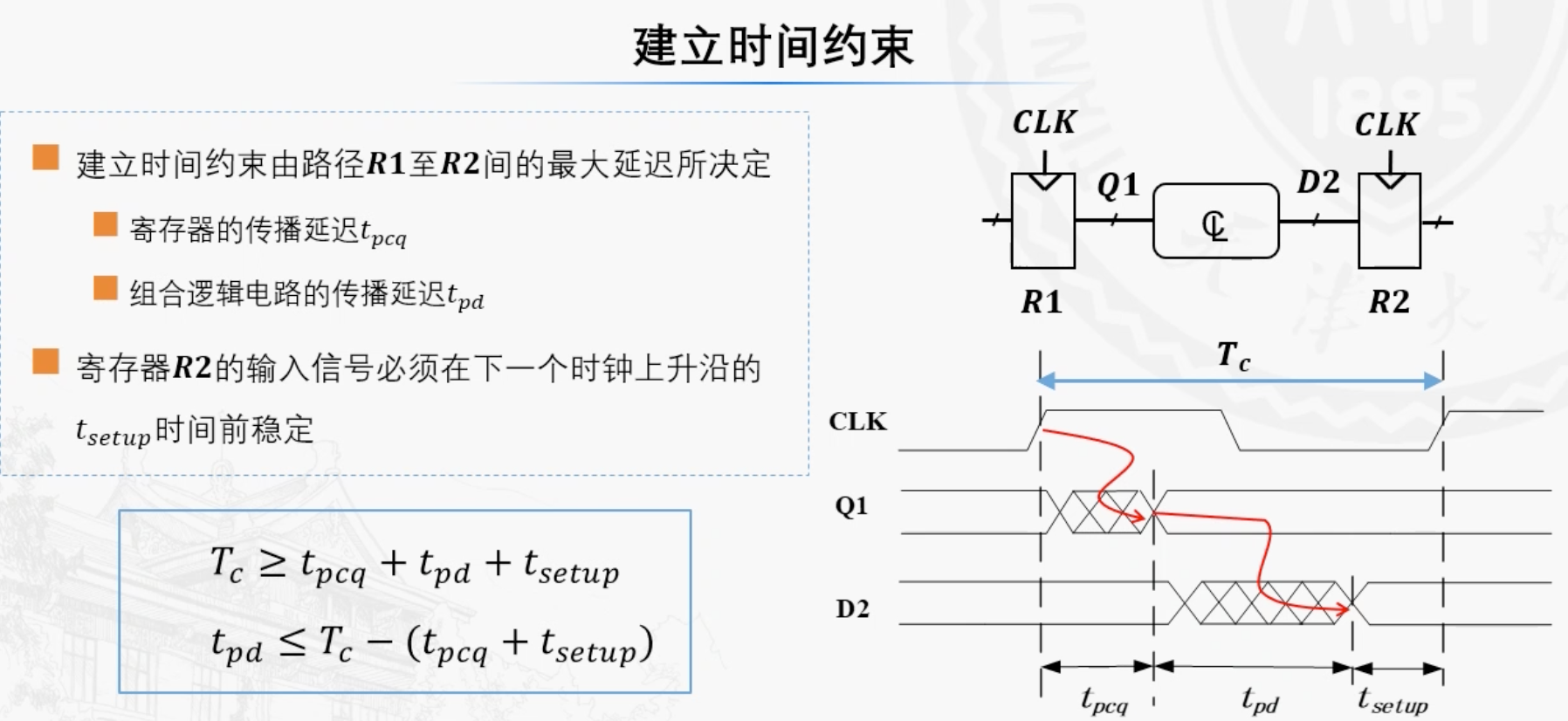
对于寄存器而言，要保证信号的稳定采样，还需要对保持时间进行约束
\[ t_{cd} \ge t_{hold} - t{ccq} \]

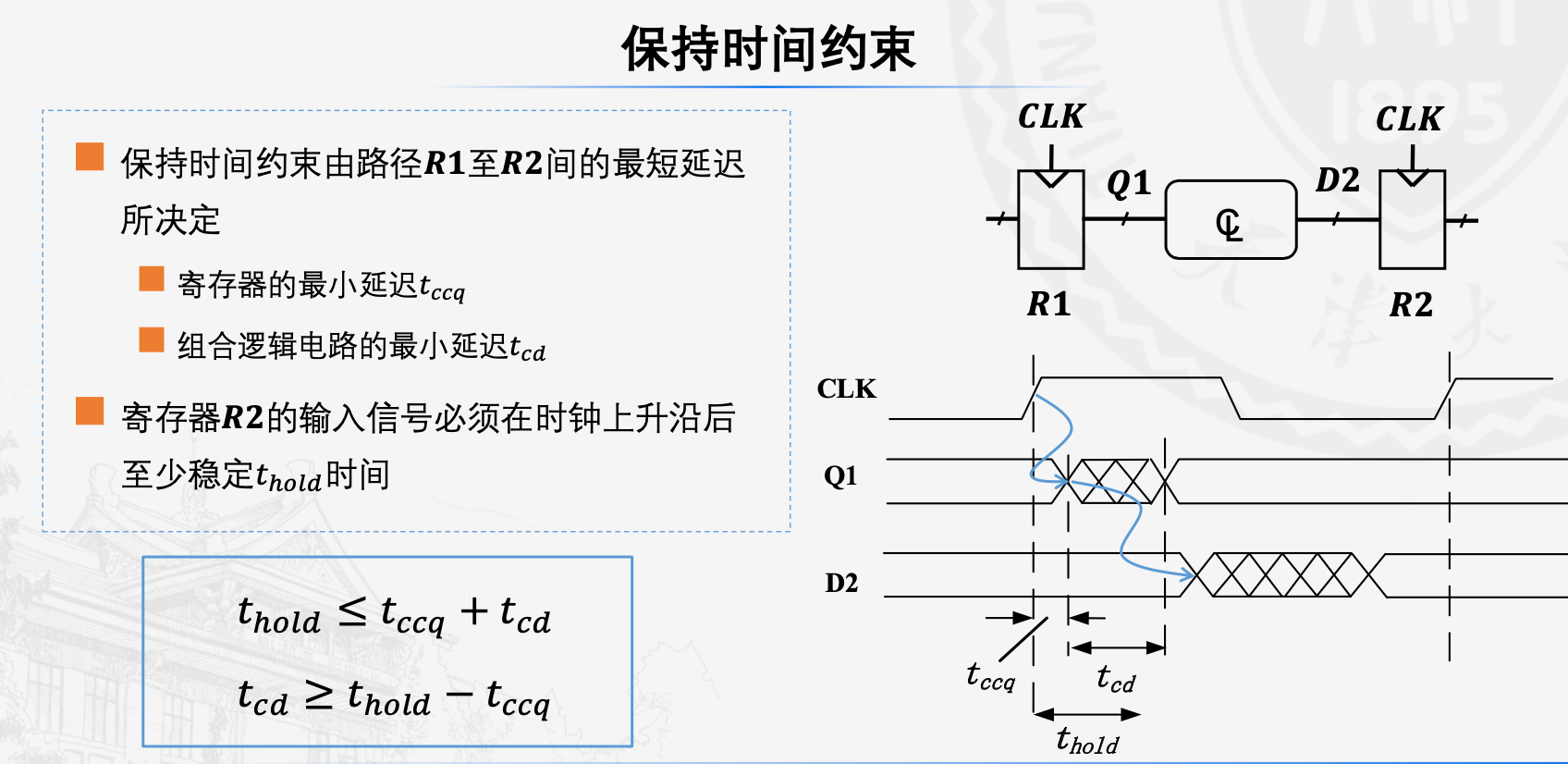
这里保持时间结束时，要保证组合逻辑电路的最小延迟时间还没有结束，不然D2开始变化，会导致R2的采样不稳定，图中的这一个时钟周期，可以理解为上一个图的后一个时钟周期。

时序问题例题

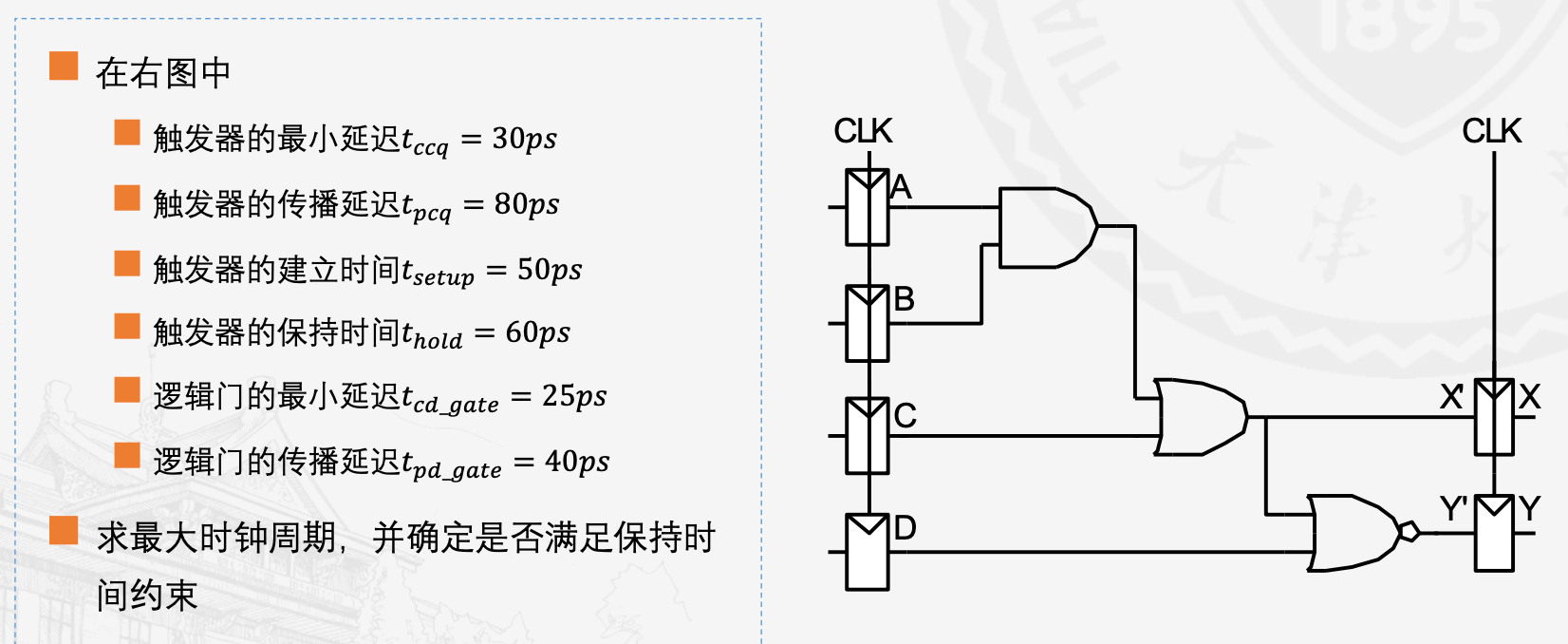
image-20210623135558808

这里就结合到了我们之前讲的两个路径：关键路径和最短路径。

首先求最大时钟周期，即关键路径时间，即从A到Y的寄存器经过3个门的时间，要计算经过这3个门的时间，当然都使用门的传播延迟，即有40ps * 3，所以组合逻辑延迟$t_{cd} = 120ps$，同时，一个周期里，应当是A出发的信号到达Y'，所以有A的传播延迟和Y'的建立时间，即我们之前说的建立时间约束$Tc \ge t_{pcq} + t_{cd} + t_{setup}$，时钟周期最小为250ps

然后保持时间约束要求$t_{hold} \le t_{cd} + t_{ccq}$，显然60比25+30大，所以是违反了保持时间约束的。

文章作者: X Mεl0n

文章链接: http://www.zrzz.site/posts/812c5abc/

学习笔记